Understanding Logarithmic Learning

Logarithmic learning is an empirical model of how different industries reduce cost and time as they acquire more experience and adopt more efficient technologies for their processes. From the various models of learning, the logarithmic is one of the most used because of its simplicity and the good fitting it has with data collected along decades on many major industries.

The formula for logarithmic learning is depicted in the image below, where lg is the base 2 logarithm, n is the current experience and n₀ is the base experience, i.e., the experience required before any learning really happens, and λ is the learning parameter.

The value of φ is the reduction factor, i.e., the factor by which the cost (or time) will be reduced.

In order to have a more intuitive understanding of this formula let's introduce:

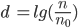
Then w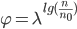e have:

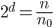
or:

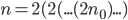
where the number 2 occurs d times. Of course, this transformation only makes sense when d is an integer number. However, if we restrict our attention to such cases we find that d would be the number of doublings required to reach n from the experience base n₀.

In other words, the logarithmic exponent of the learning parameter λ is the number of times we have doubled our initial experience.

In the particular case where n = 2n₀ we see that φ becomes λ. This means that λ is the reduction factor we will obtain the first time we double our initial experience.

Summarizing we have:

1. The learning parameter λ is the reduction factor of the first doubling.
2. We can reduce the cost (or time) in a factor of λ as many times as we have doubled the initial experience.

Assume for instance that we expect to reduce our cost by a factor of 0.8 after having drilling 100 wells and that our experience base is 50. Which would be the cost reduction factor after having drilled 400 wells?

We know that λ = 0.8 and that n₀ = 50. Therefore, since 400 = 2(2(2.50)), the number of doublings would be 3, and the reduction factor would be 0.8 x 0.8 x 0.8 = 0.512.